Pada kesempatan kali ini saya akan menjelaskan mengenai konsep vektor Operasi pada Vektor di Ruang-n Euclides, Sifat, Contoh Serta Pembuktian pada Pemrograman R . Berikut ilustrasi vektor
Vektor dalam matematika adalah sebuah objek yang mempunyai panjang (besar/nilai) dan arah.
Ilustrasi Vektor di Ruang 2
Ilustrasi Vektor di Ruang 3
Pada gambar di atas arah panah menunjukan arah vektor dan panjang panah
menyatakan besarnya. Ekor panah dinamakan titik awal (initial point) dan ujung panah
dinamakan titik akhir (terminal point) dari vektor.
Notasi Vektor (Cara Penulisannya)
Penulisan vektor dalam matematika dapat dinyatakan dalam huruf kecil tebal misalnya
a, k dan z. Namun pada kenyataanya tangan kita tidak terbiasa menulis tebal-tipis huruf
sehingga akan sedikit merepotkan, sehingga ada alternatif penulisan lainnya yakni
Catatan: Dua vektor atau lebih dikatakan sama jika dan hanya jika arah dan panjangnya
sama. Pada gambar di atas vektor k dan z
sebab memiliki arah dan panjang yang sama, walaupun letaknya berbeda.
Operasi Vektor
Jika sebelumnya penggambaran vektor dari sudut pandang geometri. Nah, sekarang
karena pembahasannya sudah sampai operasi vektor maka kita akan coba bahas
konsep vektor secara analitis. Sehingga nantinya kita juga mendapatkan konsep penjumlahan, pengurangan, perkalian vektor secara analitis.
Pada gambar di atas kita dapat menyatakan vektor :
Artinya, secara analitis jika kita punya vektor v berada pada ruang-2 (ruang dimensi 2
atau kita gunakan bidang kartesius) maka kita dapat menuliskannya :
Contohnya pada gambar di atas, vektor a
mempunyai titik awal di titik (9, -2) dan titik akhir di titik (6,5) sehingga berdasarkan
persamaan di atas maka a dapat kita tuliskan :
Kemudian bagaimana jika vektornya berada pada ruang-3 (ruang dimensi 3) ?
Jangan khawatir, hal tersebut tidak jauh berbeda dengan konsep yang di ruang-2.
Misalkan kita punya v
Dengan :
Ilustrasi :
Ilustrasi Vektor Di
Ruang 3
Maka dapat kita tuliskan :
Catatan : Apabila vetor v adalah sebuah vektor yang titik awalnya di titik pusat
koordinat (Contoh pada ruang-2 (0,0) maka vektor v biasa disebut sebagai vektor
posisi
Contoh 1
Misalkan kita punya vektor a dan b sebagai berikut :
Tentukan hasil a + b?
Penyelesaian
Secara geometri kita geser vektor
Sedangkan secara analitis maka :
Pembuktian pada pemrograman R :
install.packages("mise")
library(mise)
mise()
A=matrix(c(3,2),1,2)
B=matrix(c(-7,5),1,2)
hasil1=A+B
Run varabel variabel tersebut dan hasilnya seperti gambar dibawah ini
Contoh 2
Misalkan vektor a dan b didefinisikan sebagai berikut:
Tentukan hasil dari a+3b
Penyelesaian:
- secara geometris
kemudian kita guanakan sifat operasi penjumlahan sehingga kita peroleh
- secara analitis
Jika meneyelesaikannya secara analitis maka dapat kita tuliskan:
Sehingga berdasarkan sifat operasi penjumlahan vektor dan perkalian vektor dengan skalar maka kita dapatkan:
Pembuktian pada pemrograman R :
install.packages("mise")
library(mise)
mise()
A=matrix(c(6,5),1,2)
B=matrix(c(4,0),1,2)
hasil1=A+B
hasil2=A+(3*B)
hasil3=A+(3%*%B)
hasil4=A+B+B+B
Run varabel variabel tersebut dan hasilnya seperti gambar dibawah ini :
Contoh 3
Misalkan diberikan dua buah vektor di ruang-2 yang didefinisikan sebagai berikut :
Tentukan hasil dari a-b
Penyelesaian :
Ingat kembali bahwa jika suatu vektor dikali dengan skalar yang bernilai negatif maka
hasil perkaliannya berupa vektor yang arahnya berlawanan dengan vektor yang
dikalikan.
Pembuktian pada Pemrograman R
install.packages("mise")
library(mise)
mise()
A=matrix(c(6,5),1,2)
B=matrix(c(-4,7),1,2)
Perkalian Vektor dengan Vektor
Operasi ini terbagi menjadi 2 bagian, pertama Perkalian Titik (dot product) dan yang kedua adalah Perkalian Proyeksi dalam Vektor (cross product).
Penyelesaian :
Cara pertama (menggunakan persamaan pertama)
Cara kedua dengan menggunakan konsep determinan matriks :
Pembuktian pada Pemrograman R
install.packages("mise")
library(mise)
mise()
Cross <- function(x, y, i=1:3) {
To3D <- function(x) head(c(x, rep(0, 3)), 3)
x <- To3D(x)
y <- To3D(y)
Index3D <- function(i) (i - 1) %% 3 + 1
return (x[Index3D(i + 1)] * y[Index3D(i + 2)] -
x[Index3D(i + 2)] * y[Index3D(i + 1)])
}
A=matrix(c(1,2,3),1,3)
B=matrix(c(3,2,1),1,3)
hasil1=A*B #x1x2 + y1y2 +z1z2
hasil1=sum(hasil1)
hasil2=Cross(A,B)
Simpulan Vektor Rn / Ruang-n Euclides
Operasi standar pada ruang-n euclides ( Rn) meliputi penjumlahan vektor dan perkalian
vektor dengan skalar. Selain itu, berlaku juga operasi hasil kali titik (dot product). Lalu
bagaimana dengan hasil kali silang (cross product)? Dalam ruang-n euclides, cross
product berlaku dengan baik di R3.
Penyelesaian :
- Berdasarkan operasi penjumlahan vektor maka kita peroleh :
- Masih dengan cara yang sama, kita juga dapatkan :
-
Hal tersebut dikarenakan pada penjumlahan dua buah matriks, haruslah mempunyai ordo yang sama.
Hasil Kali Titik (Dot Product)
Contoh dan Penyelesaian
Penyelesaian :
Pertama, berdasarkan definisi hasil kali titik kita peroleh :
Kedua, berdasarkan sifat perkalian vektor dengan skalar kita peroleh :
Pembuktian pada Pemrograman R
install.packages("mise")
library(mise)
mise()
u=matrix(c(1,2,3,4),1,4)
v=matrix(c(8,7,6,5),1,4)
w=matrix(c(3,2,1),1,3)
P1=sum(u*v)
P2=sum(u*v)*w
P3=sum(u*w)
Kenapa ketika Run P3 muncul pesan "Error in u * w : non-conformable arrays"? Sudah dijelaskan di atas bahwa karena hasil kali titik (dot product) di Rn adalah sebuah fungsi yang mengolah
atau mengkawankan dua vektor di Rn. Maka jika u = (1,2,3,4) d = di R4 dan w = (3,2,1) di R3 akibatnya :
Bagaimana? sedikit tercerahkan dengan materi kali ini? semoga membantu. :)
Operasi pada Vektor di Ruang-n Euclides, Sifat, Contoh Serta Pembuktian pada Pemrograman R
 Reviewed by Amir Hamzah Dinnillah
on
Juni 29, 2020
Rating:
Reviewed by Amir Hamzah Dinnillah
on
Juni 29, 2020
Rating:
 Reviewed by Amir Hamzah Dinnillah
on
Juni 29, 2020
Rating:
Reviewed by Amir Hamzah Dinnillah
on
Juni 29, 2020
Rating:



























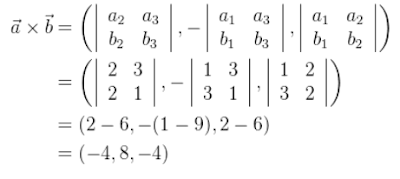

















Tidak ada komentar: